טרפז הוא מרובע אשר לו שתי צלעות נגדיות מקבילות (אין שום תנאי על הצלעות האחרות). אם גם שתי הצלעות האחרות מקבילות זו לזו, הרי שהטרפז הוא מקבילית. במקורות רבים מוגדר הטרפז בצורה מצמצמת, כ"מרובע אשר לו זוג אחד בלבד של צלעות מקבילות" (ראו הרחבה בהמשך ערך זה), ולפי הגדרה זו המקבילית איננה טרפז.
בטרפז שאיננו מקבילית, שתי הצלעות המקבילות נקראות "בסיסי הטרפז" (לפעמים קרויה "בסיס" רק הצלע הארוכה יותר), ושתי האחרות "שוקי הטרפז". בטרפז כזה ניתן להמשיך את שוקי הטרפז עד שהן ייפגשו בנקודה, ובצורה זו נוצר משולש המכיל את הטרפז. זוג הזוויות הסמוכות לכל אחד מהבסיסים נקרא זוויות בסיס.
מרובע הוא טרפז אם ורק אם יש לו שתי זוויות סמוכות שסכומן 180 מעלות.
טרפז שווה שוקיים - טרפז נקרא שווה-שוקיים אם זוויות הבסיס שלו שוות. בטרפז שווה-שוקיים שתי השוקיים שוות באורכן ושני האלכסונים שווים. טרפז שבו שתי השוקיים שוות באורכן הוא שווה-שוקיים או מקבילית.
את שטח הטרפז ניתן לחשב כמכפלת המרחק בין שתי הצלעות המקבילות (זהו גובה הטרפז) והממוצע החשבוני של אורך הצלעות הללו. דבר זה מוביל לנוסחה הידועה של שטח משולש, כאשר אנו מחשיבים את המשולש כטרפז שאחת הצלעות המקבילות כווצה לנקודה בודדת (כלומר אורך 0). נוסחאות לחישוב שטח
טרפז כלשהו (כאשר a,b - בסיסים ; c,d צלעות):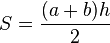
h - גובה הטרפז
a - אורך בסיס אחד
b - אורך בסיס שני
קישורים:
טרפז שווה שוקיים
האלכסונים בטרפז שווה שוקיים שווים זה לזה
הזוויות שליד כל בסיס בטרפז שווה שוקיים שוות זו לזו.
אם האלכסונים בטרפז שווים זה לזה אז הוא טרפז שווה שוקיים.
קטע אמצעים בטרפז
קטע היוצא מאמצע שוק אחת בטרפז ומקביל לבסיסים חוצה גם את השוק השניה
קטע האמצעים בטרפז מקביל לבסיסים ושווה למחצית סכומם.
בטרפז שאיננו מקבילית, שתי הצלעות המקבילות נקראות "בסיסי הטרפז" (לפעמים קרויה "בסיס" רק הצלע הארוכה יותר), ושתי האחרות "שוקי הטרפז". בטרפז כזה ניתן להמשיך את שוקי הטרפז עד שהן ייפגשו בנקודה, ובצורה זו נוצר משולש המכיל את הטרפז. זוג הזוויות הסמוכות לכל אחד מהבסיסים נקרא זוויות בסיס.
מרובע הוא טרפז אם ורק אם יש לו שתי זוויות סמוכות שסכומן 180 מעלות.
טרפז שווה שוקיים - טרפז נקרא שווה-שוקיים אם זוויות הבסיס שלו שוות. בטרפז שווה-שוקיים שתי השוקיים שוות באורכן ושני האלכסונים שווים. טרפז שבו שתי השוקיים שוות באורכן הוא שווה-שוקיים או מקבילית.
את שטח הטרפז ניתן לחשב כמכפלת המרחק בין שתי הצלעות המקבילות (זהו גובה הטרפז) והממוצע החשבוני של אורך הצלעות הללו. דבר זה מוביל לנוסחה הידועה של שטח משולש, כאשר אנו מחשיבים את המשולש כטרפז שאחת הצלעות המקבילות כווצה לנקודה בודדת (כלומר אורך 0). נוסחאות לחישוב שטח
טרפז כלשהו (כאשר a,b - בסיסים ; c,d צלעות):
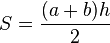
h - גובה הטרפז
a - אורך בסיס אחד
b - אורך בסיס שני
קישורים:
טרפז שווה שוקיים
האלכסונים בטרפז שווה שוקיים שווים זה לזה
הזוויות שליד כל בסיס בטרפז שווה שוקיים שוות זו לזו.
אם האלכסונים בטרפז שווים זה לזה אז הוא טרפז שווה שוקיים.
קטע אמצעים בטרפז
קטע היוצא מאמצע שוק אחת בטרפז ומקביל לבסיסים חוצה גם את השוק השניה
קטע האמצעים בטרפז מקביל לבסיסים ושווה למחצית סכומם.


