הצגת רשומות עם תוויות משולש ישר זוית. הצג את כל הרשומות
הצגת רשומות עם תוויות משולש ישר זוית. הצג את כל הרשומות
יום שבת, 1 בפברואר 2014
יום שבת, 29 בספטמבר 2012
משפט פיתגורס - הוכחה בעזרת אלגברה והשוואת שטחים
הוכחת משפט פיתגורס בדרך אלגברית
ע"פ משפט פיתגורס במשולש ישר זוית סכוםריבועי הניצבים שווה לריבוע היתר, כלומר:
לפנינו ריבוע גדול המורכב מארבעה משולשים זהים ישרי זוית abc , וריבוע קטן שצלעו היא היתר c כלואבריבוע הגדול עם המשולשים.
שטח כל הריבוע הגדול :
שטח ארבעה משולשים קטנים:
שטח ריבוע קטן:
השוואת שטחים: שטח ריבוע גדול שווה לשטחי ארבעה משולשים וריבוע קטן:
נפתח ונקבל

קיבלנו כי סכום ריבועי הניצבים שווה לריבוע היתר
ע"פ משפט פיתגורס במשולש ישר זוית סכוםריבועי הניצבים שווה לריבוע היתר, כלומר:
לפנינו ריבוע גדול המורכב מארבעה משולשים זהים ישרי זוית abc , וריבוע קטן שצלעו היא היתר c כלואבריבוע הגדול עם המשולשים.
שטח כל הריבוע הגדול :
שטח ארבעה משולשים קטנים:
שטח ריבוע קטן:
השוואת שטחים: שטח ריבוע גדול שווה לשטחי ארבעה משולשים וריבוע קטן:
נפתח ונקבל
קיבלנו כי סכום ריבועי הניצבים שווה לריבוע היתר
יום שלישי, 25 בספטמבר 2012
משפט פיתגורס - "סכום שטחי הריבועים, הבנויים על הניצבים במשולש ישר זווית, שווה לשטח הריבוע הבנוי על היתר"
משפט פיתגורס הוא משפט גאומטרי מפורסם, המתאר את היחס בין שלוש צלעותיו של משולש ישר-זווית. המשפט קובע כי "סכום שטחי הריבועים, הבנויים על הניצבים במשולש ישר זווית, שווה לשטח הריבוע הבנוי על היתר" (הניצבים הם שתי צלעות הזווית הישרה, והיתר הוא הצלע הארוכה של המשולש). או בניסוח פורמלי: אם אורכי הניצבים במשולש ישר-זווית הם  ו-
ו- , ואורך היתר הוא
, ואורך היתר הוא  , אז:
, אז: 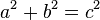 .
.
דוגמא:
נתון משולש ישר זוית שאורכי ניצביו הם 3, 4, מצא את אורך היתר
אורך היתר c:

אורך היתר c שווה 5.
 הוכחת הנשיא גרפילד למשפט פיתגורס
הוכחת הנשיא גרפילד למשפט פיתגורס
ישנו משולש ישר זוית שניצביו a, b והיתר c.
בונים ממשולש זה וזה לו טרפז ישר זוית ומחשבים את שטחו בשני אופנים.
מצד אחד, הוא שווה ל- , כיוון ששטח טרפז שווה למכפלת הגובה במחצית מסכום
, כיוון ששטח טרפז שווה למכפלת הגובה במחצית מסכום
הבסיסים.
מצד שני הוא שווה ל- כי הוא שווה לסכום שטחם של שני המשולשים האפורים עם
כי הוא שווה לסכום שטחם של שני המשולשים האפורים עם
המשולש שביניהם הלבן
מהשוואת שני הביטויים שהתקבלו, המייצגים את אותו השטח, מתקבל משפט פיתגורס.

 ו-
ו- , ואורך היתר הוא
, ואורך היתר הוא  , אז:
, אז: 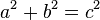 .
.דוגמא:
נתון משולש ישר זוית שאורכי ניצביו הם 3, 4, מצא את אורך היתר
אורך היתר c:
אורך היתר c שווה 5.
 הוכחת הנשיא גרפילד למשפט פיתגורס
הוכחת הנשיא גרפילד למשפט פיתגורסישנו משולש ישר זוית שניצביו a, b והיתר c.
בונים ממשולש זה וזה לו טרפז ישר זוית ומחשבים את שטחו בשני אופנים.
מצד אחד, הוא שווה ל-
הבסיסים.
מצד שני הוא שווה ל-
המשולש שביניהם הלבן
מהשוואת שני הביטויים שהתקבלו, המייצגים את אותו השטח, מתקבל משפט פיתגורס.
תוויות:
הוכחת משפט פיתגורס,
יתר,
משולש ישר זוית,
משפט פיתגורס,
ניצב
יום שבת, 15 בספטמבר 2012
בעיה פתורה בטריגונומטריה 4 יח' - משולש ישר זוית בתוך טרפז ישר זוית
שאלה בטריגונומטריה 4 יחידות
פתרון
 שטח טרפז שווה למכפלת סכום בסיסיו בגובה לחלק לשתיים, כלומר אם בסיסי הטרפז הם a ו- b וגובה הטרפז הוא h אזי שטח הטרפז S = (a + b)*h/2
שטח טרפז שווה למכפלת סכום בסיסיו בגובה לחלק לשתיים, כלומר אם בסיסי הטרפז הם a ו- b וגובה הטרפז הוא h אזי שטח הטרפז S = (a + b)*h/2
במקרה של טרפז ישר זוית כמו בסקיצה:
הבסיסים הם הצלעות AD , BC והגובה היא הצלע CD
נחשב את הצלעות AD, CD , BC
מציאת AD - משולש ADM ישר זוית לכן:
מציאת BC - זוית M1 שווה לזוית (סכום שתיהן וזוית AMD שווה 90 מעלות ולכן הן שוות)
(סכום שתיהן וזוית AMD שווה 90 מעלות ולכן הן שוות)

מציאת CD
CD = DM + CM

שטח הטרפז S

פתרון
 שטח טרפז שווה למכפלת סכום בסיסיו בגובה לחלק לשתיים, כלומר אם בסיסי הטרפז הם a ו- b וגובה הטרפז הוא h אזי שטח הטרפז S = (a + b)*h/2
שטח טרפז שווה למכפלת סכום בסיסיו בגובה לחלק לשתיים, כלומר אם בסיסי הטרפז הם a ו- b וגובה הטרפז הוא h אזי שטח הטרפז S = (a + b)*h/2במקרה של טרפז ישר זוית כמו בסקיצה:
הבסיסים הם הצלעות AD , BC והגובה היא הצלע CD
נחשב את הצלעות AD, CD , BC
מציאת AD - משולש ADM ישר זוית לכן:
מציאת BC - זוית M1 שווה לזוית
מציאת CD
CD = DM + CM
שטח הטרפז S
יום רביעי, 30 במאי 2012
מבחן מיצב כיתה ח תשע"א פתרון שאלה 21
 שאלה 21
שאלה 21 לפניכם סרטוט של מחומש ABCDE המורכב מריבוע ABDE וממשולש ישר-זווית BCD.
א. מה שטח הריבוע ABDE? הַציגו את דרך הפתרון:
נמצא תחילה את אורך צלע BD של הריבוע ABDE, ע"פ משפט פיתגורס.
משולש BCD ישר זוית (זוית C ישרה) לכן סכום ריבועי הניצבים BC, ו- CD שווה לריבוע היתר BD:
או בהצבה ופתרון:
שטח ריבוע שווה לריבוע צלע מצלעותיו השוות, בעצמה:
שטח הריבוע :
ב. מה שטח המחומש ABCDE? הַציגו את דרך הפתרון:
פתרון סעיף ב
שטח המחומש ABCDE מורכב משטח הריבוע ABDE ושטח המשולש ישר הזוית BCD. נמצא את שטח הריבוע ושטח המשולש, נחבר אותם, ונקבל את שטח המחומש.
שטח ריבוע ABDE -מצאנו בסעיף א:
שטח המשולש BCD - שטח משולש שווה למחצית מכפלת צלע בגובה לאותה הצלע. כאשר המשולש ישר זוית, הניצבים מהווים צלעות וגבהים אחד לשני, לכן שטח משולש ישר זוית שווה למחצית מכפלת ניצביו.
שטח משולש BCD:
שטח המחומש ABCDE הוא סכום שטח הריבוע ושטח המשולש: 91.5 = 74 + 17.5
ג. מה היקף המחומש ABCDE?
פתרון סעיף ג
היקף המחומש P שווה לסכום צלעותיו:
התשובה הנכונה היא מספר 3.
קישורים:
יום שני, 24 באוקטובר 2011
הוכח כי הגובה ליתר במשולש ישר זווית שווה למכפלת הניצבים לחלק ליתר
 נתון משולש ישר זווית ABC , זווית ACB ישרה
נתון משולש ישר זווית ABC , זווית ACB ישרהנדרש להוכיח כי הגובה ליתר h שווה למכפלת הניצבים a,b לחלק ביתר c
או: h=ab/c
הוכחה
נחשב את שטח המשולש בשני דרכים ונשווה ביניהם:
שטח המשולש הוא מחצית מכפלת הניצבים: S=ab/2
שטח המשולש מחושב גם כמחצית מכפלת היתר בגובה ליתר: S=ch/2
לכן: ab/2=ch/2
ab=ch
לכן הגובה ליתר: h=ab/c
מ.ש.ל
שטח המשולש הוא מחצית מכפלת הניצבים: S=ab/2
שטח המשולש מחושב גם כמחצית מכפלת היתר בגובה ליתר: S=ch/2
לכן: ab/2=ch/2
ab=ch
לכן הגובה ליתר: h=ab/c
מ.ש.ל
תוויות:
גובה ליתר,
יתר,
משולש ישר זוית,
ניצב,
שטח משולש
יום שבת, 22 באוקטובר 2011
הוכחת משפט בגיאומטריה: הניצב במשולש ישר זווית הוא הממוצע הגיאומטרי של היתר והיטלו של ניצב זה על היתר
יום שלישי, 11 באוקטובר 2011
בעיה פתורה בגיאומטריה: שני מלבנים זהים ומשולש ישר זווית שווה שוקיים
 המרובעים ABCD ו- EFCG הם מלבנים.
המרובעים ABCD ו- EFCG הם מלבנים.נתון BC = CG , FC = DC
הוכח המשולש ACE הוא ישר זווית ושווה שוקיים
הוכחה:
השיטה: מבצעים חפיפת משולשים ABC ו- CFE. מהחפיפה נועים שוויונות הצלעות AC, EF וסכום הזוויות ACB, ECF תשעים מעלות.
חפיפת משולשים ABC ו- CFE
1. CD = AB - צלעות נגדיות במלבן ABCD שוות
2. CD = FC - נתון
3. AB = FC - נובע מ- 1 ו-2
4. CG = AB - צלעות נגדיות במלבן EFCG שוות
5. CG = BC - נתון
6. AB = BC - נובע מ-4 ו-5
7. זווית ABC = זווית EFC = זוויות ישרה - כל הזוויות במלבן ישרות
8. משוויונים 3,6,7 נובע כי משולש ABC חופף למשולש CFE צ.ז.צ
מהחפיפה נובע:
EC = AC - מ.ש.ל. 1
9. זווית FCE = זווית CAB - נובע מהחפיפה 8
10. זווית ACB + זווית CAB = זווית ישרה - סכום הזוויות החדות במשולש ישר זוית ABC שווה 90 מעלות
מ-9 ו- 10 נובע:
11. זווית ACB + זווית FCE = זווית ACE = זווית ישרה - הצבה - מ.ש.ל 5
יום שבת, 17 בספטמבר 2011
בעיה פתורה בגיאומטריה - אנכים לשוקיים במשולש ש"ש
 |
בעיה פתורה בגיאומטריה - אנכים לשוקיים במשולש שווה שוקיים |
נתון משולש שווה שוקיים AB = AC
BD ו- CE הם גבהים לשוקיים במשולש, BD מאונך ל- AC, ו- CE מאונך ל- AB
א. נוכיח שמשולשים BDC ו- CEB חופפים:
שני המשולשים הם ישרי זווית לפיכך נדרשים עוד שני שיוויונים במשולשים להוכיח חפיפתם.
זהות ראשונה: זווית CBE = זווית BCD - זוויות בסיס במשולש שווה שוקיים ABC שוות
זהות שניה: BC = BC - צלע משותפת
מכאן: משולשים BDC ו- CEB חופפים
מ.ש.ל א'
ב. נוכיח ש- DE||BC באמצעות משפט תאלס הפוך:
שני ישרים (BC, DE) המקצים על שוקי זווית (BAC) קטעים פרופורציונים (AE/BE = AD/DC) , מקבילים זה לזה.
(1) AB = AC - נתון
(2) BE = CD - נובע מהחפיפה שהוכחה ב- א
לכן:
(3) AE = AD , נובע מ- (1) ו- (2): חיסור גדלים שווים מגדלים שווים נותן גדלים שווים
AE/BE = AD/DC נובע מ- (2) ו- (3) חלוקת גדלים שווים מגדלים שווים נותן מנות שוות
לכן
DE||BC - משפט תאלס הפוך:
שני ישרים (BC, DE) המקצים על שוקי זווית (BAC) קטעים פרופורציונים (AE/BE = AD/DC) , מקבילים זה לזה.
מ.ש.ל ב
ג. נוכיח ש: AE*AC = AD*AB
נוכיח דימיון משולשים ABC, AED
זווית ABC = זווית AED - מתאימות מקבילים DE||BC (הוכח בסעיף ב) , חותך AB
זווית ACB = זווית ADE - מתאימות מקבילים DE||BC (הוכח בסעיף ב) , חותך AC
זווית A = זווית A - משותפת
מכאן משולשים ABC, AED דומים - משולשים ששלוש זוויותיהם (או שניים מהזוויות) שוות, דומים
מהדימיון נובע: AE/AB = AD/AC - יחסי צלעות מתאימות במשולשים דומים
מכאן AE*AC = AD*AB
מ.ש.ל
יום ראשון, 11 בספטמבר 2011
יום רביעי, 7 בספטמבר 2011
הגובה ליתר במשולש ישר זווית הוא הממוצע הגאומטרי של היטלי הניצבים על היתר
מוכיחים דימיון משולשים ABD, ACD ע"פ שיוויונים בין הזוויות.
מהדימיון נובע: AD/BD = CD/AD, ומכאן הנדרש להוכחה: AD*AD = BD*CD

קישורים:
במשולש ישר זווית שזוויותיו החדות הן 30 ו- 60 מעלות, הניצב שמול ה- 30 מעלות שווה למחצית היתר.
אם במשולש ישר זווית אחד הניצבים שווה למחצית היתר אז הזווית שמול הניצב שווה 30.
במשולש ישר זווית התיכון ליתר שווה למחצית היתר.
משולש שבו אחד התיכונים שווה למחצית הצלע אותה הוא חוצה, הוא משולש ישר זווית.
הניצב במשולש ישר זווית הוא הממוצע הגיאומטרי של היתר והיטלו של ניצב זה על היתר.
מהדימיון נובע: AD/BD = CD/AD, ומכאן הנדרש להוכחה: AD*AD = BD*CD

קישורים:
במשולש ישר זווית שזוויותיו החדות הן 30 ו- 60 מעלות, הניצב שמול ה- 30 מעלות שווה למחצית היתר.
אם במשולש ישר זווית אחד הניצבים שווה למחצית היתר אז הזווית שמול הניצב שווה 30.
במשולש ישר זווית התיכון ליתר שווה למחצית היתר.
משולש שבו אחד התיכונים שווה למחצית הצלע אותה הוא חוצה, הוא משולש ישר זווית.
הניצב במשולש ישר זווית הוא הממוצע הגיאומטרי של היתר והיטלו של ניצב זה על היתר.
יום רביעי, 6 באפריל 2011
יום שבת, 5 במרץ 2011
יום ראשון, 20 בפברואר 2011
שטח משולש ישר זוית במערכת צירים

פתרון:
 סעיף א
סעיף אנוכיח תחילה כי משולש ABC ישר זוית
1. הקטע AB נמצא על הישר y=2
2. הקטע BC נמצא על הישר x = -3
3. הקטעים AB ו- BC מאונכים - מונחים על ישרים מאונכים
3. הקטעים AB ו- BC מאונכים - מונחים על ישרים מאונכים
4. AB = 8 - הפרש הקורדינאטות x של הנקודות A, B
5. באופן דומה BC = 6
6. שטח המשולש: ABC = 6*8/2 = 24 משולש
5. באופן דומה BC = 6
6. שטח המשולש: ABC = 6*8/2 = 24 משולש
סעיף ב
הנקודה D נמצאת על הישר x = -3 , בנוסף היא באמצע הקטע BC
לכן שיעור ה- y של הנקודה D יהיה ממוצע הקורדינטה y של B ו-C
[2+(-4)] /2 = -1
שיעור הנקודה ( D(-3, -1
סעיף ג
המשולש ABD ישר זוית מאחר וזוית B ישרה כפי שהוכח בסעיף א.
AB = 8 - הוכח בסעיף א.
BD = 3 אורך הקטע BD הוא הפרש ה- Yים של B, D כלומר : 2-(-1) = 3
השטח של המשולש ABD = AB*BD/2 = 3*8/2 = 12
סעיף ד
שטח המשולש ACD שווה להפרש שטחי המשולשים: ABC, ו- ABD
כלומר 12
תוויות:
גיאומטריה,
מערכת צירים,
משולש ישר זוית,
שטח משולש
יום שישי, 4 בפברואר 2011
משולש 30 60 90 - הניצב מול זוית 30 מעלות שווה למחצית היתר
הוכח כי במשולש ישר זוית שזויותיו 30 , 60 , 90 מעלות , הניצב מול זוית 30 מעלות שווה למחצית היתר
הוכחה
 |
משולש 30 60 90 - הניצב מול זוית 30 מעלות שווה למחצית היתר |
תוויות:
הוכחה,
הוכחת משפט בגיאומטריה,
יתר,
משולש 30 60 90,
משולש ישר זוית,
ניצב
הירשם ל-
רשומות (Atom)











