הוכחת משפט פיתגורס בדרך אלגברית
ע"פ משפט פיתגורס במשולש ישר זוית סכוםריבועי הניצבים שווה לריבוע היתר, כלומר:
לפנינו ריבוע גדול המורכב מארבעה משולשים זהים ישרי זוית abc , וריבוע קטן שצלעו היא היתר c כלואבריבוע הגדול עם המשולשים.
שטח כל הריבוע הגדול :
שטח ארבעה משולשים קטנים:
שטח ריבוע קטן:
השוואת שטחים: שטח ריבוע גדול שווה לשטחי ארבעה משולשים וריבוע קטן:
נפתח ונקבל

קיבלנו כי סכום ריבועי הניצבים שווה לריבוע היתר
ע"פ משפט פיתגורס במשולש ישר זוית סכוםריבועי הניצבים שווה לריבוע היתר, כלומר:
לפנינו ריבוע גדול המורכב מארבעה משולשים זהים ישרי זוית abc , וריבוע קטן שצלעו היא היתר c כלואבריבוע הגדול עם המשולשים.
שטח כל הריבוע הגדול :
שטח ארבעה משולשים קטנים:
שטח ריבוע קטן:
השוואת שטחים: שטח ריבוע גדול שווה לשטחי ארבעה משולשים וריבוע קטן:
נפתח ונקבל
קיבלנו כי סכום ריבועי הניצבים שווה לריבוע היתר


 ו-
ו- , ואורך היתר הוא
, ואורך היתר הוא  , אז:
, אז: 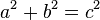 .
.

