משפט פיתגורס הוא משפט גאומטרי מפורסם, המתאר את היחס בין שלוש צלעותיו של משולש ישר-זווית. המשפט קובע כי "סכום שטחי הריבועים, הבנויים על הניצבים במשולש ישר זווית, שווה לשטח הריבוע הבנוי על היתר" (הניצבים הם שתי צלעות הזווית הישרה, והיתר הוא הצלע הארוכה של המשולש). או בניסוח פורמלי: אם אורכי הניצבים במשולש ישר-זווית הם  ו-
ו- , ואורך היתר הוא
, ואורך היתר הוא  , אז:
, אז: 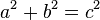 .
.
דוגמא:
נתון משולש ישר זוית שאורכי ניצביו הם 3, 4, מצא את אורך היתר
אורך היתר c:

אורך היתר c שווה 5.
 הוכחת הנשיא גרפילד למשפט פיתגורס
הוכחת הנשיא גרפילד למשפט פיתגורס
ישנו משולש ישר זוית שניצביו a, b והיתר c.
בונים ממשולש זה וזה לו טרפז ישר זוית ומחשבים את שטחו בשני אופנים.
מצד אחד, הוא שווה ל- , כיוון ששטח טרפז שווה למכפלת הגובה במחצית מסכום
, כיוון ששטח טרפז שווה למכפלת הגובה במחצית מסכום
הבסיסים.
מצד שני הוא שווה ל- כי הוא שווה לסכום שטחם של שני המשולשים האפורים עם
כי הוא שווה לסכום שטחם של שני המשולשים האפורים עם
המשולש שביניהם הלבן
מהשוואת שני הביטויים שהתקבלו, המייצגים את אותו השטח, מתקבל משפט פיתגורס.

 ו-
ו- , ואורך היתר הוא
, ואורך היתר הוא  , אז:
, אז: 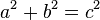 .
.דוגמא:
נתון משולש ישר זוית שאורכי ניצביו הם 3, 4, מצא את אורך היתר
אורך היתר c:
אורך היתר c שווה 5.
 הוכחת הנשיא גרפילד למשפט פיתגורס
הוכחת הנשיא גרפילד למשפט פיתגורסישנו משולש ישר זוית שניצביו a, b והיתר c.
בונים ממשולש זה וזה לו טרפז ישר זוית ומחשבים את שטחו בשני אופנים.
מצד אחד, הוא שווה ל-
הבסיסים.
מצד שני הוא שווה ל-
המשולש שביניהם הלבן
מהשוואת שני הביטויים שהתקבלו, המייצגים את אותו השטח, מתקבל משפט פיתגורס.






