בעיה פתורה בגיאומטריה - משולש שווה שוקיים חסום במעגל ומשיקים לקודקודיו

בעיה פתורה בגיאומטריה - משולש שווה שוקיים חסום במעגל ומשיקים לקודקודיו

שאלה פתורה בגיאומאטריה - משולש שווה צלעות

שאלה


פתרון

משפט בגיאומטריה: היחס בין שטחי משולשים דומים שווה לריבוע יחס הדמיון בין המשולשים

קישורים:

גבהים מתאימים במשולשים דומים מתייחסים זה לזה כיחס הצלעות המתאימות.

חוצי זוויות מתאימות במשולשים דומים מתייחסים זה לזה כמו יחס הצלעות המתאימות.

תיכונים מתאימים במשולשים דומים מתייחסים זה לזה כיחס הצלעות המתאימות.

משפט בגיאומטריה: תיכונים מתאימים במשולשים דומים מתייחסים זה לזה כמו יחס הצלעות המתאימות

משפט בגיאומטריה: זוויות מתאימות במשולשים דומים מתייחסים זה לזה כמו יחס הצלעות המתאימות

הוכחת משפט בגיאומטריה - שני מיתרים נחתכים במעגל, מחלקים זה את זה כך שמכפלת קטעי מיתר אחד שווה למכפלת קטעי המיתר השני

הוכחת משפט בגיאומטריה: גבהים מתאימים במשולשים דומים מתייחסים זה לזה כיחס הצלעות המתאימות

הגובה ליתר במשולש ישר זווית הוא הממוצע הגאומטרי של היטלי הניצבים על היתר

מוכיחים דימיון משולשים ABD, ACD ע"פ שיוויונים בין הזוויות.
מהדימיון נובע: AD/BD = CD/AD, ומכאן הנדרש להוכחה: AD*AD = BD*CD

קישורים:

במשולש ישר זווית שזוויותיו החדות הן 30 ו- 60 מעלות, הניצב שמול ה- 30 מעלות שווה למחצית היתר.
אם במשולש ישר זווית אחד הניצבים שווה למחצית היתר אז הזווית שמול הניצב שווה 30.
במשולש ישר זווית התיכון ליתר שווה למחצית היתר.
משולש שבו אחד התיכונים שווה למחצית הצלע אותה הוא חוצה, הוא משולש ישר זווית.
הניצב במשולש ישר זווית הוא הממוצע הגיאומטרי של היתר והיטלו של ניצב זה על היתר.

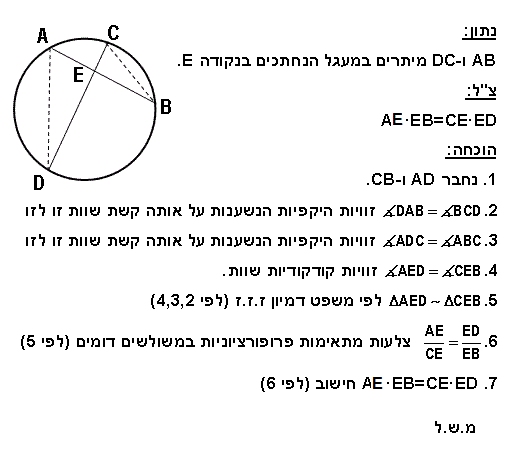
פרופורציה במעגל - אם מנקודה מחוץ למעגל יוצאים שני קווים חותכים למעגל אז מכפלת חותך אחד בחלקו החיצוני שווה למכפלת חותך שני בחלקו החיצוני

שיטת ההוכחה:

מוכיחים דימיון משולשים ABE, ו- ACD, באמצעות זווית משותפת A, וזוויות היקפיות שוות (ז.ז.ז.). מהדימיון נובע הנדרש להוכיח: AB*AD = AC*AE